算法分析

From this, I can learn smart algorithm and solutions I will never come up with myself.

二分(Binary)

设置伐木机的高度使在达到指标的前提下尽量少砍

int check(vector<int>& trees,int H){
    int sum=0;
    for (int tree:trees){
        if (tree>H){//筛选所有高于标准的树
            sum+=tree-H;
        }
    }
    return sum;
}

int adjustHeight(vector<int>& trees,int goal){//value-based banary
    int left=0,right=trees.back();//back()指向最后一个元素
    int result=0;
    while(left<=right){
        int mid=left+(right-left)/2;//mid需要不断更新,定义在循环里
        int collected=check(trees,mid);
        if (collected>=goal){
            result=mid;
            left=mid+1;
        }else {
            right=mid-1;
        }
    }
    return result;
}

Why value-based binary?

考虑极端情况:{1,1,1,…,1,1,4}.如果是基于索引的查找,mid在大部分时候会维持1不变.相反,采用高度的中值效率更高也更符合实际情况.

Why is the if statement written this way?

一定能正常结束.达成指标时,记录结果并判断能否再抬升高度:如果抬升将使指标无法达成,右界前移,反之左界后移,直至边界重合.此时返回的结果为最后一次执行if语句时mid的值,即最后一次满足指标的情况.(建议手动模拟一下)

贪心(greedy algorithm)

在无时间冲突的情况下,尽量多参加比赛.比赛的起止点由数轴表示.例如三场比赛(0,2) (2,4)(1,3),则最多参加2场.

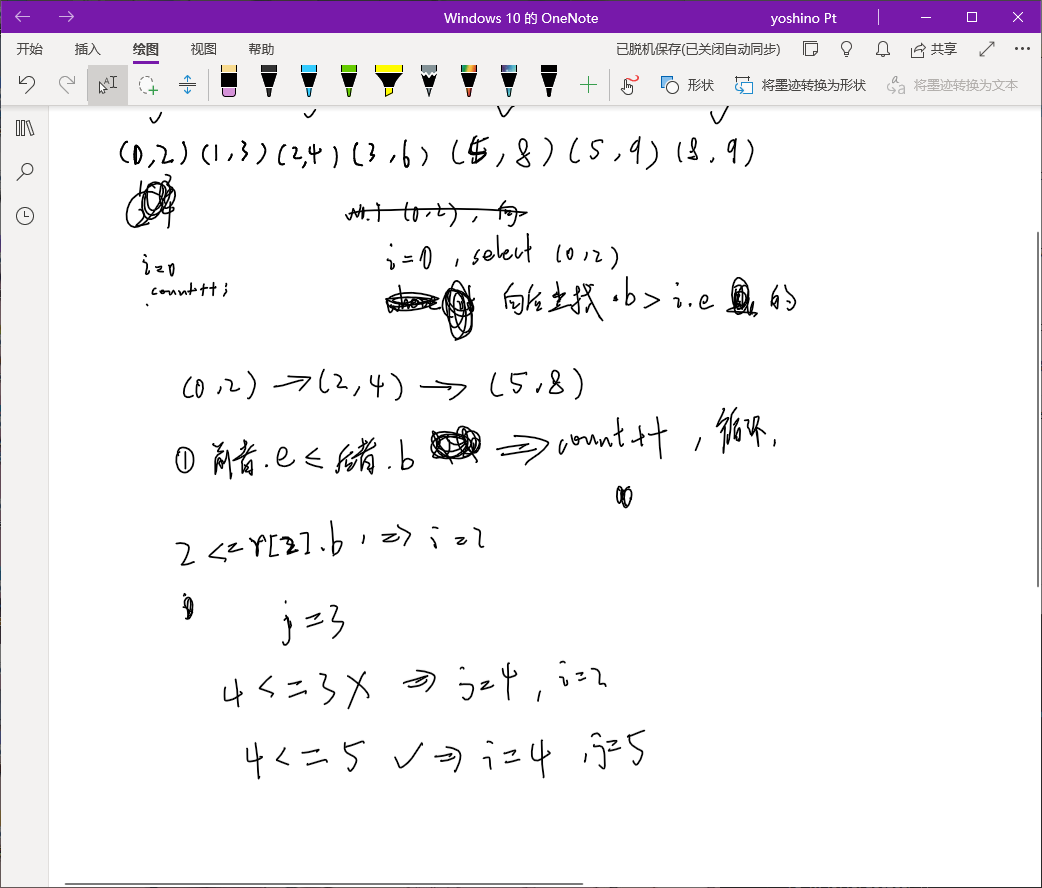
最开始的判断:先按开始点排序,在开始点相同时选择最短的,然后从其结束点开始下一场…不断循环记录场数至最后一个最短的开始点.

正确策略：

1. 按结束点排序：将比赛按结束时间从小到大排序。如果结束时间相同，可以任意处理开始时间（因为结束时间决定了是否冲突）。
2. 逐个选择不冲突的比赛：从最早结束的比赛开始，选择一场比赛，然后跳过所有与之冲突的比赛，从下一场不冲突的比赛继续。

这种方法的直觉是：尽量腾出时间为后续比赛提供更多可能性。

为什么是贪心

• 当局部最优选择始终可以导致全局最优解时，贪心算法能保证得到最优解

主要算法实现

需求:每次选择结束时间靠前的比赛,在不冲突的前提下选择下一场比赛.记录选择过的比赛的场数.

在寻找思路时,我列出了一组数据:(0,2) (1,3) (24) (3,6) (5,8) (5,9) (8,9).并手动模拟了运行过程:

int maxRaces(vector<race>& races,int n){
    int i=0,count=0;
    for (int j=1;j<n;j++){
        if (races[i].end<=races[j].begin){
            count++;
            i=j;
        }
    }
    return count;
}

完整程序https://github.com/Pottery114514/ciallo/blob/main/Algorithm/how_much_race.cpp

Maximum Subarray Sum(Kadane’s Algorithm)

找到最大的子数组和.

具体思路

Traverse over the array from left to right and for each element, find the maximum sum among all subarrays ending at that element. The result will be the maximum of all these values.

//Maximum Subarray Sum(Kadane’s Algorithm)
#include <bits/stdc++.h>
using namespace std;
int maxSubarraySum(vector<int>& arr){
    int sum=0,currentMax=0;
    for (int i=0;i<arr.size();i++){
        sum=max(sum+arr[i],arr[i]);//继续累加or重开.后者大于前者意味着上一个sum为负数
        currentMax=max(sum,currentMax);//记录当前最大值
    }
    return currentMax;
}

int main(){
    vector<int> array;
    int num;

    //set 0 as sentinel value that terminates input.
    while (cin>>num&&num!=0){
        array.push_back(num);
    }
    
    cout<<maxSubarraySum(array);
    return 0;
}

另一种形式,用于不存在空数组的情况

int findMax(vector<int>& array) {
    int maxSum = INT_MIN; // 初始化为负无穷
    int currentSum = 0;

    for (int num : array) {
        currentSum += num;          // 累加当前元素
        maxSum = max(maxSum, currentSum); // 更新最大和
        if (currentSum < 0) {       // 如果当前和小于 0，丢弃之前的累加结果
            currentSum = 0;
        }
    }

    return maxSum;
}

Explanation

• max()很好,简化逻辑很有用.

查找

输入 n 个不超过10^9的单调递增的非负整数，然后进行 m 次询问。对于每次询问，给出一个整数 q，输出这个数字在序列中第一次出现的编号，如果没有找到的话输出 −1 。

Approach

第一次尝试了for循环遍历查找,理所当然的超时了.

向AI询问后,给出的答案竟是……哈希表??

以下是二分查找(Binary Search),类似于查字典.

Implement

基于索引(Index-Based)的二分搜索

避免在每次比较期间重新计算索引, 最大限度地减少循环内的操作(minimizes operations inside the loop)

int BinarySearch(const vector<int>& numbers,int target){
	int left=0,right=numbers.size()-1;
	while(left<right){
		int mid=left+(right-left)/2;
		if (numbers[mid]<target) left=mid+1;
		else right=mid;
	}
	if (left<numbers.size()&&numbers[left]==target)
		return left+1;
	return -1;
}

• 关于If语句中的判断条件

  left < numbers.size()：

  • 是一种安全检查，防止意外越界。
  • 如果完全确信不会越界（理论和实践都验证），可以省略它。

  numbers[left] == target ：

  • 为什么不是检查numbers[right]?在二分查找中，形成[left,right)区间,退出时left是唯一可能点.

• 这里numbers有序,const将其定义为常量防止意外更改(read-only),也有助于理解函数意图.

• 为什么仍加取址符(Reference)&?其直接访问对象(仍能直接修改元素),避免复制整个容器以减少开销. 也就是说, 未加&时每次调用函数时都会复制整个容器,产生不必要的开销.

  The name of a vector, points to its first element or acts like the base address of the data it manages.

  However, this address does not mean you are referencing the vector object itself (which includes metadata like size, capacity, etc.). It refers to the memory of the elements it stores.

Extra

• if-else与if的比较

  //combine the conditions,only one comparison per iteration.
  if (numbers[mid] == target) 
      return mid;
  else if (numbers[mid] < target) 
      left = mid + 1; 
  else 
      right = mid; 
  
  //每次迭代中都会执行三次比较
  if (target < numbers[mid]) right = mid;
  if (target > numbers[mid]) left = mid + 1;
  if (target == numbers[mid]) return mid;

  前者避免了不必要的检查.

Usestd::lower_bound Instead of Binary Search

• 可能会减少少量时间

  #include <algorithm>  // For std::lower_bound
  
  int Find(const vector<int>& numbers, int target) {
      auto it = lower_bound(numbers.begin(), numbers.end(), target);
      if (it != numbers.end() && *it == target) 
          return it - numbers.begin();
      return -1;
  }

• Storing results in a vector and printing them in one go can help reduce I/O overhead.
• 如果不是递增数组,可以定义结构体来将数字与排序前的索引绑定.